Fractals: Plants and Stochastic L-systems
Sat 18 January 2020 by A Silent Llama
One particular type of fractal that I find compelling is the ‘plant fractal’. These are fractals that model plant growth.
In fact Aristid Lindenmayer, the man L-systems are named after, was a biologist studying the growth patterns of plants and he devised the L-system approach because it helped model those patterns.
Branching
Naturally the first thing we are faced with is the problem of branching. How do we instruct our turtle to draw a stem and branch and then to return to where it started to continue the stem? We could, I suppose, create a rule that creates a branch and then reverses itself to get the turtle back to where it started but that sounds too complicated.
Lets imagine an extension of our L-system rules. We add the following to our rule alphabet: [ and ]. Think of these exactly like parentheses in English. A sentence can have a main topic (and then have some other information added on) and return to that topic after the parenthetical statement. In the same way a turtle can draw something and then arrive at some instructions enclosed in our [] ‘parentheses’. It will execute the instructions in the parentheses and then return to what it was doing before.
The question is how to implement this? We need to supply our turtle with some sort of memory. Let’s do that:
// turtle.rs
struct Position {
x: i32,
y: i32,
angle: f32,
}
We add a Position struct that saves the exact position and angle of our turtle at some point in time. We then extend our turtle to be able to ‘remember’ Positions:
// turtle.rs
pub struct Turtle {
pen: bool,
x: i32,
y: i32,
width: u32,
height: u32,
angle: f32,
stack: Vec<Position>,
canvas: RgbImage,
}
We’ve added a stack member to our turtle struct. This is simply a Vector of Positions. We’ll be using it as a stack - when the turtle wishes to remember a position it will place a new Position struct on the stack with its current bearings. If the turtle has to branch again it add will another Position on to the stack. The key point is that each time the turtle finishes a parenthesis command it needs to go back to the most recent position. This will be always be at the top of the stack which we can easily pop off to get the turtle back to where it started.
We’ll need the following new turtle commands:
// turtle.rs
// -- snip --
pub fn push(self: &mut Self) {
self.stack.push(Position {
x: self.x,
y: self.y,
angle: self.angle,
});
}
pub fn pop(self: &mut Self) {
// The 'if let' statement might look weird if you're used to languages
// that don't have it. In this case it works like Python's new 'walrus' operator:
// we only assign to pos when self.stack.pop() actually returns something.
// If it returns nothing (None) then we don't do anything. We're using
// Rust's Option type here which is an enum that defines _something_ as Some(var)
// and nothing as None. The if let statement below reads as follows:
// If we got _some_thing off the stack then reset our position. Otherwise
// do nothing.
// In general the if let can match any variant of a rust enum not just Option.
if let Some(pos) = self.stack.pop() {
self.x = pos.x;
self.y = pos.y;
self.angle = pos.angle;
}
}
// -- snip
The push method simply saves the current position to the top of the stack. The pop method gets the last Position the turtle pushed and then ‘teleports’ the turtle to that position by overriding it’s x, y and angle members.
Lastly we just need to add the [] symbols to our instructions:
// main.rs
// -- snip --
for c in instructions.chars() {
match c {
'F' => turtle.forward(fractal.forward),
'G' => turtle.forward(fractal.forward),
'+' => turtle.left(fractal.angle),
'-' => turtle.right(fractal.angle),
'[' => turtle.push(),
']' => turtle.pop(),
_ => {
// Ignore - we allow characters that aren't drawing commands.
}
}
}
// -- snip --
We’re now in a position to draw a plant fractal!
Let’s try the following:
{
"axiom": "F",
"rules": {"F": "FF-[-F+F+F]+[+F-F-F]"},
"iterations": 4,
"angle": 22,
"forward": 12,
"start_x": 300,
"start_y": 700,
"start_angle": 270
}
This produces:

Which is definitely plant like. If we look at the rules we can see that we draw the ‘stem’ with the first two F rules. We then turn and draw a branch. We then undo the turn and branch again in a different direction and repeat the process in the usual way.
Here’s another one we can try:
{
"axiom": "X",
"rules": {"F": "FF",
"X": "F-[[X]+X]+F[+FX]-X"},
"angle": 22.5,
"iterations": 5,
"forward": 5,
"start_x": 130,
"start_y": 450,
"start_angle": 270.0,
"height": 475,
"width": 250
}
And we get:

Stochastic Rules
While this looks pretty it lacks an important property of a real plant: plants don’t grow in exactly the same pattern every time! To model plants a little more realistically we’re going to have to introduce Stochastic Rules.
Now the word ‘stochastic’ might sound complicated but it just means that we are going to be adding some randomness into our rules. Stochastic is a nice mathematical sounding word that basically just means ‘random’.
A stochastic rule is an expansion of our normal rule type. A normal rule looks like this:
F -> F+F
Which simply means replace F with F+F. We’ll expand this to look something like:
F -> (50%) F+F
-> (50%) G
This means there’s a 50% chance we’ll replace F with F+F and a 50% chance we’ll replace it with G .
We’ll need to extend our fractal definition file to able to handle this. We still want our previous files to work so we’re going to use some nice features serde to implement this.
Firstly we’re going to allow different rule types:
// fractal_def.rs
// -- snip --
#[derive(Deserialize)]
pub struct StochasticRule {
pub probability: f32,
pub rule: String
}
#[derive(Deserialize)]
#[serde(untagged)]
pub enum Rules {
BasicRules(HashMap<char, String>),
StochasticRules(HashMap<char, Vec<StochasticRule>>)
}
// -- snip --
We create a StochasticRule to represent a single probability/rule pair. We then create a Rules enum with two variants: BasicRules and StochasticRules. The BasicRules variant is what we’ve been using so far. The StochasticRules variant is almost the same except now instead of a single rule matching we have a list of rules and probabilities. We amend our main FractalDefinition struct like this:
#[derive(Deserialize)]
pub struct FractalDefinition {
// -- snip --
pub rules: Rules,
// -- snip --
}
We’ve marked our enum as ‘untagged’ for serde. Serde allows us to ‘tag’ variants for better performance but since we only read this file once at startup it isn’t necessary. By marking the enum as ‘untagged’ serde will automatically work out which variant fits.
We’ll need a random number generator:
// Cargo.toml
[dependencies]
// Add:
rand = "0.7"
We then need to handle this variant when we draw:
// -- snip
use rand::prelude::*;
// -- snip --
let mut rng = rand::thread_rng();
for c in instructions.chars() {
match &fractal.rules {
Rules::BasicRules(rules) => {
if rules.contains_key(&c) {
buffer.push_str(&rules[&c]);
} else {
buffer.push(c);
}
},
Rules::StochasticRules(rules) => {
if rules.contains_key(&c) {
for r in &rules[&c] {
let random_number: f32 = rng.gen();
// We generate a number between 0 and 1. Our test
// to see if we should use a rule is simple: if our
// random number is less than our probability then
// we apply the rule. As our probability gets bigger
// the likelihood of it being applied gets bigger too.
if random_number < r.probability {
buffer.push_str(&r.rule);
break;
}
}
} else {
buffer.push(c);
}
}
}
// -- snip --
We can now define our stochastic rules in a json file like this:
{
"axiom": "F",
"rules": {"F": [{"probability": 0.33, "rule": "F[+F]F[-F]F"},
{"probability": 0.33, "rule": "F[+F]F"},
{"probability": 0.34, "rule": "F[-F]F"}]},
"iterations": 6,
"angle": 30,
"forward": 7,
"start_x": 400,
"start_y": 700,
"start_angle": 270
}
Let’s see what we get:
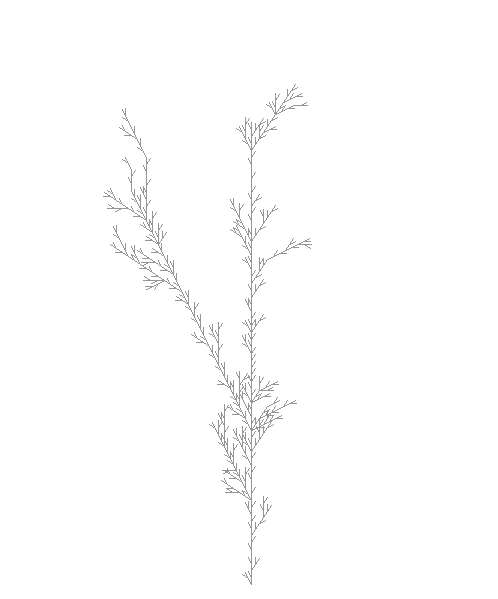
You will very likely get something completely different. You can see that the resulting fractal is a lot more chaotic and ‘organic’ than our previous tries. In fact I had to run the generator a few times before I got one I thought looked good enough.
Planting Seeds
A big problem with randomly generating our images is that if we find one we really like we can never generate it again! We have no idea what random numbers were used. There is a way to overcome this problem - we’ll grow our plants using seeds.
Random Number Generators (RNGs) are mathematical functions that generate sequences of numbers that ‘look’ random. There’s a lot of math behind the word ‘look’ in that sentence but I’m not going to get into the technical details. Suffice it to say that the numbers they generate are random enough even though they’re technically defined by a precise formula and could be easily predicted if you knew the formula and it’s starting point. RNGs are a little like fractals because they take an initial starting value (called a ‘seed’ which is a really convenient word when you’re creating plant fractals!) and then apply a function to that value. They then iterate exactly like a fractal by using the last value to generate the next one.
So all we need to do to get make sure we can re-generate a plant is make sure we supply a seed.
// fractal_def.rs
// -- snip --
#[derive(Deserialize)]
pub struct FractalDefinition {
// -- snip --
seed: Option<u64>,
// -- snip --
}
We can now use the seed for our RNG:
// main.rs
// -- snip --
let mut rng = match fractal.seed {
Some(seed) => StdRng::seed_from_u64(seed),
None => StdRng::seed_from_u64(random()),
};
Now we can supply the seed and this time we’ll get the same output every time we generate:
{
"axiom": "F",
"rules": {"F": [{"probability": 0.33, "rule": "F[+F]F[-F]F"},
{"probability": 0.33, "rule": "F[+F]F"},
{"probability": 0.34, "rule": "F[-F]F"}]},
"iterations": 6,
"angle": 30,
"forward": 7,
"start_x": 400,
"start_y": 700,
"start_angle": 270,
"seed": 2563,
"width": 400,
"height": 750
}
We now have a reproducible plant:
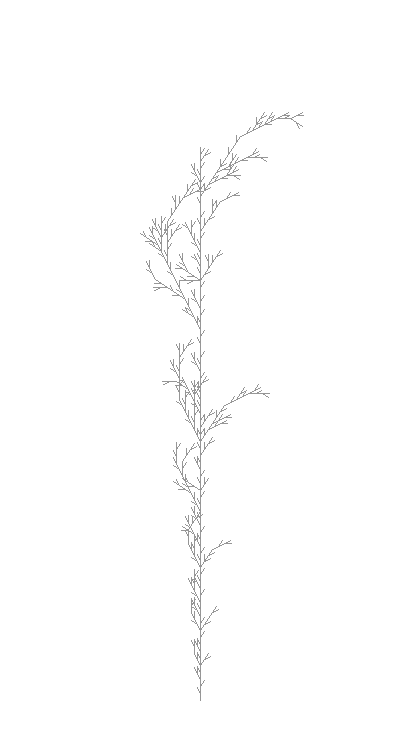
And to top it off an animation of the drawing process. Notice how the turtle jumps back to the stem as it completes each branch:

Code is on Gitlab.
References
I’ve been relying heavily on the book The Algorithmic Beauty of Plants which is a fantastic reference. Give it a look - it’s much better than any of my paltry blog posts!